nn <- neuralnet(f, data=train_Boston, hidden=c(5), linear.output=T)
# Algorithm did not converge in 1 of 1 repetition(s) within the stepmax.Neural Network Regression Models
R Packages for Neural Network Regression Models
Neural Networks method (in-sample and out-of-sample performance measure) is illustrated here. The package neuralnet and nnet are used for this purpose.
neuralnetpackage
The arguments:
- hidden: a vector of integers specifying the number of hidden neurons (vertices) in each layer.
- rep: the number of repetitions for the neural network’s training.
- startweights: a vector containing starting values for the weights. The weights will not be randomly initialized.
- linear.output: TRUE for continuous response FALSE for categorical response.
nnetpackage
The arguments:
- size: number of units in the hidden layer.
- maxit: maximum number of iterations. Default 100.
- decay: parameter for weight decay. Default 0.
- linout: TRUE for continuous response FALSE for categorical response (default)
- weights: (case) weights for each example – if missing defaults to 1.
Neural Network model for Boston housing data
For regression problems, we use neuralnet and add linear.output = TRUE when training model. In practices, the normalization and standardization for predictors and response variable are recommended before training a neural network model. Otherwise, your neural network model may not be able to converge as the following case:
I chose to use the min-max method and scale the data in the interval \([0,1]\). Other reference online: [1]
library(MASS)
data("Boston")
# Calculate the maximum values for each column in the 'Boston' dataset.
maxs <- apply(Boston, 2, max)
# Calculate the minimum values for each column in the 'Boston' dataset.
mins <- apply(Boston, 2, min)
# Normalize the 'Boston' dataset using min-max scaling:
# Each feature is centered around its minimum and scaled to the range [0, 1].
scaled <- as.data.frame(scale(Boston, center = mins, scale = maxs - mins))
# Randomly sample 90% of the dataset indices for training.
index <- sample(1:nrow(Boston), round(0.9 * nrow(Boston)))
# Create a training set from the sampled indices.
train_Boston <- scaled[index,]
# The remaining 10% of indices are used to create a test set.
test_Boston <- scaled[-index,]- Plot the fitted neural network model:
# Load the 'neuralnet' package for training neural networks.
library(neuralnet)
# Create a formula for predicting 'medv' (median house value) using all other variables in the dataset.
f <- as.formula("medv ~ .")
# Or you can do the following way that is general and will ease your pain to manually update formula:
# resp_name <- names(train_Boston)
# f <- as.formula(paste("medv ~", paste(resp_name[!resp_name %in% "medv"], collapse = " + ")))
# Train a neural network model using the training dataset 'train_Boston':
# - 'f' is the formula defining the target variable and predictors.
# - 'hidden = c(5, 3)' specifies a neural network architecture with two hidden layers (first with 5 neurons, second with 3).
# - 'linear.output = T' indicates that the output layer is not activated (appropriate for regression problems).
nn <- neuralnet(f, data = train_Boston, hidden = c(5, 3), linear.output = TRUE)
# Plot the neural network structure to visualize the trained model.
plot(nn)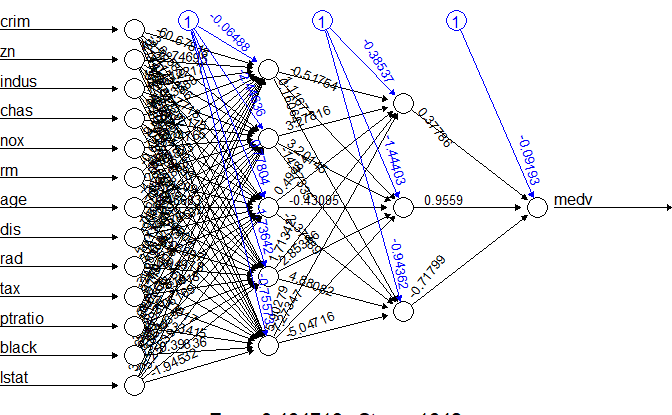
- Calculate the MSPE of the above neural network model (what is MSPE?):
pr_nn <- compute(nn, test_Boston[,1:13])
# recover the predicted value back to the original response scale
pr_nn_org <- pr_nn$net.result*(max(Boston$medv)-min(Boston$medv))+min(Boston$medv)
test_r <- (test_Boston$medv)*(max(Boston$medv)-min(Boston$medv))+min(Boston$medv)
# MSPE of testing set
MSPE_nn <- sum((test_r - pr_nn_org)^2)/nrow(test_Boston)
MSPE_nn[1] 5.826554Remark: If the testing set is not available in practice, you may try to scale the data based on the training set only. Then the recovering process should be changed accordingly.